Serendip

Web Studio

問題4.37

an-integer-between に変数名を引数として渡し、low の値を印字するように修正する。

(define (an-integer-between low high val-name)
  (require (<= low high))
  (begin
    (print val-name " is " low)
    (amb low (an-integer-between (+ low 1) high val-name))))

Ben Bitdiddle の提案する Pythagoras 三角形を生成する手続き。
an-integer-between で、変数名を渡すように修正した。

(define (a-pythagorean-triple-between low high)
  (let ((i (an-integer-between low high "i"))
        (hsq (* high high)))
       (let ((j (an-integer-between i high "j")))
            (let ((ksq (+ (* i i) (* j j))))
                 (require (>= hsq ksq))
                 (let ((k (sqrt ksq)))
                      (require (integer? k))
                      (list i j k))))))

実行結果（Ben Bitdiddle の手続きの場合）

;;; Amb-Eval input:
(define (require p)
  (if (not p) (amb)))

;;; Starting a new problem
;;; Amb-Eval value:
ok

;;; Amb-Eval input:
(define (an-integer-between low high val-name)
  (require (<= low high))
  (begin
    (print val-name " is " low)
    (amb low (an-integer-between (+ low 1) high val-name))))

;;; Starting a new problem 
;;; Amb-Eval value:
ok

;;; Amb-Eval input:
(define (a-pythagorean-triple-between low high)
  (let ((i (an-integer-between low high "i"))
        (hsq (* high high)))
       (let ((j (an-integer-between i high "j")))
            (let ((ksq (+ (* i i) (* j j))))
                 (require (>= hsq ksq))
                 (let ((k (sqrt ksq)))
                      (require (integer? k))
                      (list i j k))))))

;;; Starting a new problem 
;;; Amb-Eval value:
ok

;;; Amb-Eval input:
(a-pythagorean-triple-between 1 5)

;;; Starting a new problem i is 1
j is 1
j is 2
j is 3
j is 4
j is 5
i is 2
j is 2
j is 3
j is 4
j is 5
i is 3
j is 3
j is 4

;;; Amb-Eval value:
(3 4 5.0)

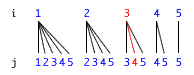
問題4.35 の Pythagoras 三角形を生成する手続き。
an-integer-between で、変数名を渡すように修正した。

(define (a-pythagorean-triple-between low high)
  (let ((i (an-integer-between low high "i")))
       (let ((j (an-integer-between i high "j")))
            (let ((k (an-integer-between j high "k")))
                 (require (= (+ (* i i) (* j j)) (* k k)))
                 (list i j k)))))

実行結果（問題4.35 の手続きの場合）

;;; Amb-Eval input:
(define (require p)
  (if (not p) (amb)))

;;; Starting a new problem
;;; Amb-Eval value:
ok

;;; Amb-Eval input:
(define (an-integer-between low high val-name)
  (require (<= low high))
  (begin
    (print val-name " is " low)
    (amb low (an-integer-between (+ low 1) high val-name))))

;;; Starting a new problem
;;; Amb-Eval value:
ok

;;; Amb-Eval input:
(define (a-pythagorean-triple-between low high)
  (let ((i (an-integer-between low high "i")))
       (let ((j (an-integer-between i high "j")))
            (let ((k (an-integer-between j high "k")))
                 (require (= (+ (* i i) (* j j)) (* k k)))
                 (list i j k)))))

;;; Starting a new problem
;;; Amb-Eval value:
ok

;;; Amb-Eval input:
(a-pythagorean-triple-between 1 5)

;;; Starting a new problem i is 1
j is 1
k is 1
k is 2
k is 3
k is 4
k is 5
j is 2
k is 2
k is 3
k is 4
k is 5
j is 3
k is 3
k is 4
k is 5
j is 4
k is 4
k is 5
j is 5
k is 5
i is 2
j is 2
k is 2
k is 3
k is 4
k is 5
j is 3
k is 3
k is 4
k is 5
j is 4
k is 4
k is 5
j is 5
k is 5
i is 3
j is 3
k is 3
k is 4
k is 5
j is 4
k is 4
k is 5

;;; Amb-Eval value:
(3 4 5)

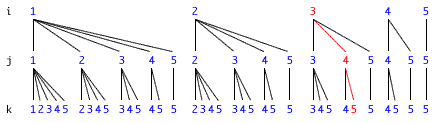
この結果から解るように、Ben の提案する手続きの方が効率的に探索している。

参考：SICP 4.3.1 Ex. 4.35 Ex. 4.36 Ex. 4.37 – nakayama-blog

計算機プログラムの構造と解釈

posted with amazlet at 08.11.07

ジェラルド・ジェイ サスマン ジュリー サスマン ハロルド エイブルソン
ピアソンエデュケーション
売り上げランキング: 6542

Amazon.co.jp で詳細を見る